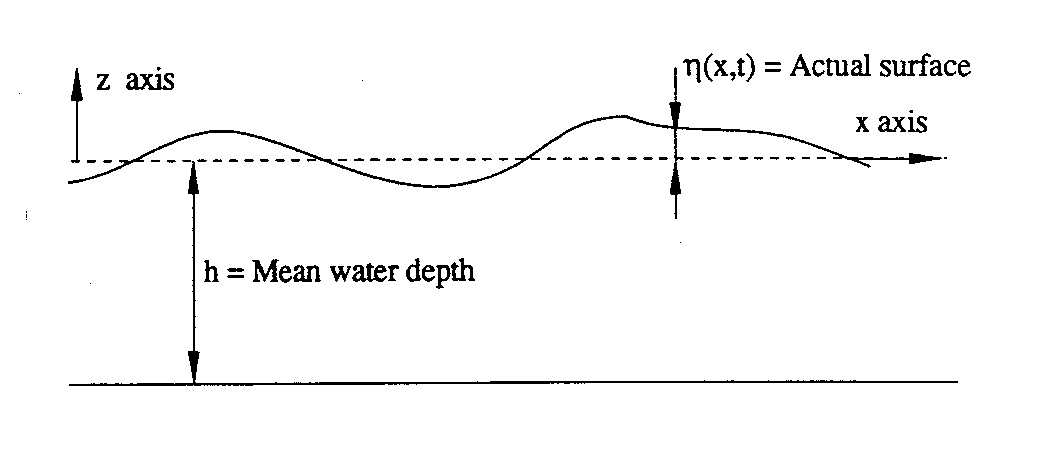
3. THE EQUATIONS FOR SURFACE WAVES
In this section we shall see how waves may occur on the surface of water in nature or in a manmade water tank. Unfortunately, it is rather difficult to derive these equations and we shall therefore not give a complete derivation, but assume some familiarity with fluid mechanics.
The water motion is governed by the laws of mechanics. These laws are all conservation laws which tell you that something is conserved. The most familiar one is mass conservation which says that mass cannot be created or disappear.
We shall first consider waves in a channel with parallel walls and horizontal bottom. We shall also assume that the waves travels along the channel and that there are no variation in the water motion across the channel.

Fig. 3.1: Waves along a channel
Since everyone have seen waves on the surface of the water, waves which propagate along the channel, is is obvious that such waves exist. The problem is then to derive how the wavelength and the period of the waves may be expressed in terms of, say the water depth, the acceleration of gravity etc.
The waves on the surface set the rest of the water into motion, and at each point, ![]() , the fluid has a velocity
, the fluid has a velocity
![]()
where z denotes the vertical coordinate measured upwards from the mean water level. We have now introduced unit vectors i, pointing along the x-axis and k, pointing along the z-axis (This k should not be confused with the wavenumber vector which we are going to use later).
Note that vectors are written with bold letters. u and w are thus the x- and the z-components of the velocity.
Water is hard to compress, and for our purpose, we will assume that this is impossible, that is, we consider water to be incompressible. In an incompressible fluid, the velocity ![]() at each point will satisfy the equation
at each point will satisfy the equation
![]()
called the equation of continuity.
In our case the y-component of the velocity, v, is assumed to be zero, that is, we do not assume any variations across the channel.
If, in addition, the fluid is considered to be irrotational, the velocity may be expressed in terms of a so-called velocity potential ![]() such that
such that
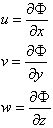
The concepts "irrotationality" and "velocity potential" are treated in courses in Fluid Mechanics, and also in about every textbook about water waves. If we introduce the velocity potential in the continuity equation
![]()
we obtain
![]()
(In the general case, we should also add a term ![]() .)
.)
This equation is a very famous partial differential equation called the Laplace equation.
It turns out that Laplace equation is all we have to know about the water motion away from the boundaries and the surface.
The bottom of the channel is not permeable to the water, and therefore the vertical water velocity at the bottom must be zero at all times:
![]()
This constitutes a relation which must hold at the boundary, and it is therefore called a boundary condition. For the moment we assume that the channel very long so that we do not have to bother about conditions and the far ends.
The conditions at the water surface are harder to obtain. It has been observed that the fluid near the surface remains near the surface during the wave motion as long as the motion is smooth. That is, unless the waves break. The first boundary condition at the free surface consists of stating this property in mathematical terms. Consider a part of the surface at two neighbouring times as indicated in Fig. 3.2.
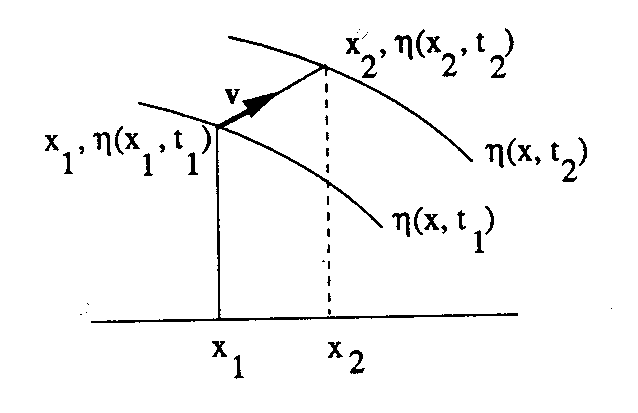
Figure 3.2: Motion of a fluid point on the free surface
The point at ![]() moves with velocity v to
moves with velocity v to ![]() during the time interval
during the time interval ![]() . Thus,
. Thus,
![]()
Let us also expand ![]() in a Taylor series:
in a Taylor series:
![]()
If this is introduced in first equation above, we obtain
![]()
Or, if we divide by ![]() and let
and let ![]() ,
,
![]()
This is the mathematical formulation of the physical condition that a fluid particle at the surface should remain at the surface at all times. It tells you something about the motion of the surface and is therefore called the kinematic boundary condition.
The other condition to be satisfied at the surface comes from the fact that the pressure ![]() at the surface must be equal to the atmospheric pressure, which we assume is constant. This condition may be derived from Bernoulli's Equation which is also treated in basic courses on Fluid Mechanics (actually, a version of Benoulli's Equation is different from the more familiar form for steady flow). The equation states that for irrotational flow
at the surface must be equal to the atmospheric pressure, which we assume is constant. This condition may be derived from Bernoulli's Equation which is also treated in basic courses on Fluid Mechanics (actually, a version of Benoulli's Equation is different from the more familiar form for steady flow). The equation states that for irrotational flow
![]()
The function ![]() is not important and may be set to an arbitrary convenient constant. If we let
is not important and may be set to an arbitrary convenient constant. If we let ![]() Bernoulli's Equation gives for the free surface:
Bernoulli's Equation gives for the free surface:
![]()
This condition, dealing with the force on the surface, is usually called the dynamic boundary condition.
All together, we have now formulated the mathematical problem which must be solved in order to find the motion of the surface:
1) Within the fluid, Laplace's equation must be satisfied
![]()
2) At the closed bottom,
![]()
3) The surface is always made up of the same fluid particles:
![]()
(has to hold at the surface ![]() ).
).
4) The pressure in the fluid at the free surface is equal to the atmospheric pressure:
![]()
(has to hold at the surface ![]() ).
).
The mathematical problem stated in (1) to (4) is very difficult. No complete solution is known, although we know a lot about special cases.
The next section will treat the case where the magnitude of ![]() is very small compared to the variations in the x-direction (For a wave we would say that the amplitude is small compared to the wavelength).
is very small compared to the variations in the x-direction (For a wave we would say that the amplitude is small compared to the wavelength).