The equations stated in the previous section are much too complicated to be solved in full generality. We are going to linearize the equation and the boundary condition, and in order to do so, we shall apply a useful technique called dimensional analysis and scaling. Actually, in most textbooks, the linearization is treated very briefly.

Assume that the typical length scale for variations in the x-direction is L (for ocean waves, L could typically be of order 100m which we write as O(100m) ). Assume further that the time scale is T. (This could be a typical wave period which for ocean waves would be around 8s.) The amplitude is of the order A, that is, . The two physical parameters in our problem are

h = the mean water depth

and

g = the acceleration of gravity.

(It turns out that water density and viscosity, which did not occur in our equations anyway, are of virtually no significance.)

From the five quantities

L, T, A, h and g

we may form three dimensionless combinations:

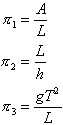
(There are other possible combinations but these turn out to be the most convenient).

The small amplitude gravity waves case is when , that is, when A << L, and gravity is essential, that is, .

The appropriate water velocity scale follows from the vertical motion of the surface. Thus the scale for |v| is A/T. Consider the kinematic condition,

.

The first term is O(A/T), the right hand side is of the same order, whereas the second term is

Since A/L is supposed to be much smaller than 1, we may neglect the second term and use the simplified kinematic condition

in the present case.

We then consider the dynamic condition:

The magnitude of is since

The first term is thus of order

The second term is of order

Thus, the second is negligible compared to the first. Finally, the last term is

since we were considering the case where

The last term is thus of the same order as the first term, and we obtain the simplified condition

Unfortunately, the simplified problem is still too difficult for us since the velocities and the potential should be taken at the free surface,- which we do not know. However,

.

since

.

In accordance with the approximations we have already done, we may neglect the term , and simply use the linearized kinematic condition

.

The h-dependence is thus gone. A similar argument also linearizes the dynamic condition:

We are now finally ready for attacking the linearized equations:

, (1)

, (2)

, (3)

(4)

We are primarily looking for solutions that are regular waves so let us first see whether (1) may have such solutions. For a given z, we thus assume that F has the form

where k, w and are unknowns and A is an amplitude which we assume is dependent of z (It is conceivable that A should depend on z). If this function is inserted into (1), we easily obtain

Shall this be fulfilled for all x and t, we must have that the term in the bracket vanishes completely. This leads to an second order ordinary linear differential equation for A which has the general solution

Equation (2) requires

,

which means that . But which vanishes at if . Thus, a possible solution which satisfies both (1) and (2) is

.

It remains to be seen whether (3) and (4) can be satisfied. Equation (4) actually gives an expression for h since

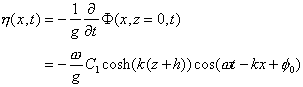
But (3) must also hold, that is,

must be equal to

Shall this last condition be true for all x- and t-s, we must have

or

This is an equation which says that w and k can not be chosen at will. For a given , only the two frequencies, w and -w which satisfies the equation are allowed. The equation is called a dispersion relation. The dispersion relation tells us how the frequency and the wavenumber are connected.

If we now let and set

we recover the familiar running regular wave for h:

.

For the potential F we obtain:

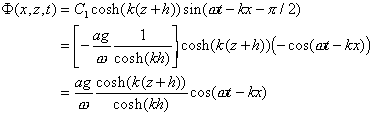
The equations for h, F and the dispersion relation represent the core of linear wave theory.