The dispersion relation says that waves with a given frequency must have a certain wavelength. For the wave the wavenumber k and w must be connected by the dispersion relation . Note that for a given k , there are two possibilites for w, namely and . This corresponds to waves going to the right and to the left, respectively. The mathematical function is shown in Fig. 5.1.

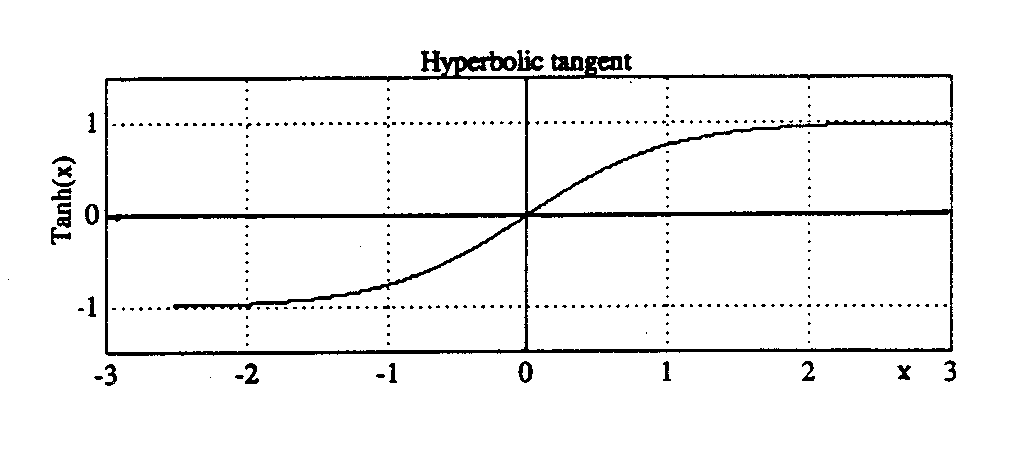
Fig. 5.1: The hyperbolic tangent, .

For small values of the argument

Moreover,

.

We recall that h is the water depth, and where l is the wavelength. Thus, . If kh is small, then h << l, that is, the water depth is much smaller than the wavelength. This corresponds to shallow water. Conversely, if kh is large, this corresponds to deep water. Let us consider the dispersion relation in these particular cases.

Now and may be replaced by kh. Thus, , or

.

In this case, we set = 1 and

Note there is a wide range of water depths which are neither shallow nor deep for a given wavelength. The rules of thumb are:

• Use the deep water expression when .

• Use the shallow water expression when

The phase velocity, cp , of a regular wave was defined as

We recall that this was, e.g. the speed of the top (crest) of the wave as it moves along. From the dispersion relation we obtain the following expression for the phase velocity

.

Let us see what this amount to in deep and shallow water. In shallow water, we obtain the somewhat surprising answer that the phase velocity is independent of both w and k:

However, the velocity is now dependent of the depth, h. Waves for which the phase velocity is constant are called non-dispersive (Light waves in vacuum and regular sound waves in air are also non-dispersive).

For deep water we obtain

.

In deep water, the speed increases with increasing wave period and wavelength. The graph below is copied from the book of K.F. Bowden. Note that as long h < , the waves move with constant speed.

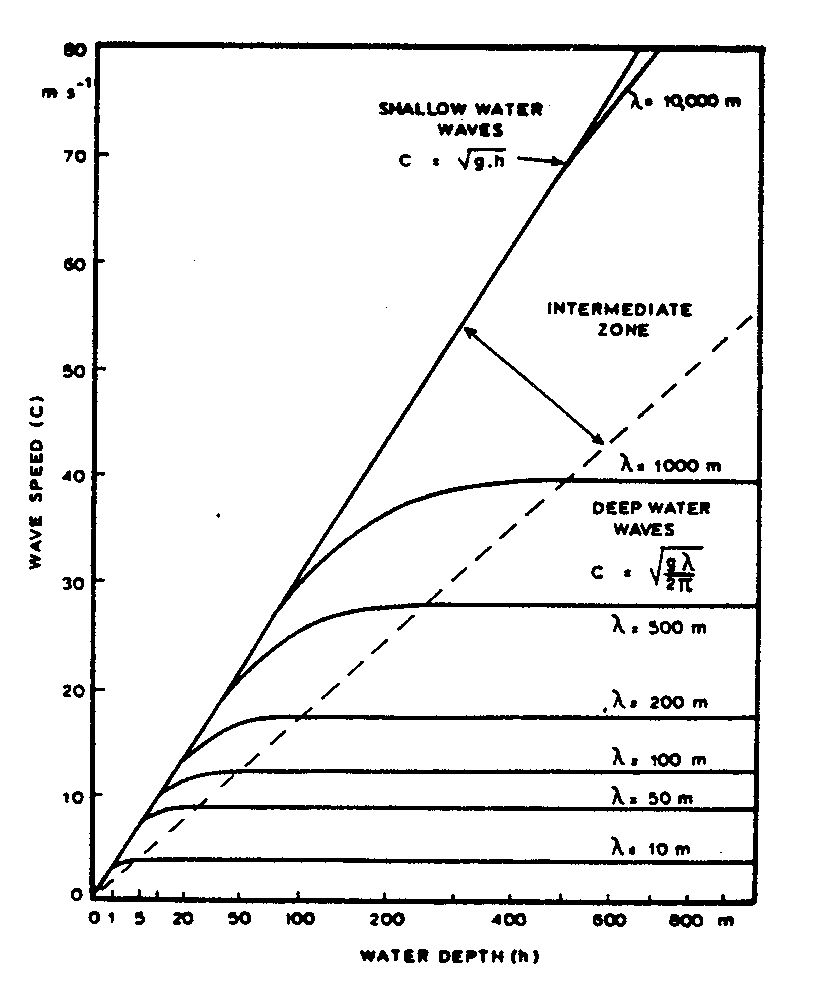
Fig. 5.2: The phase velocity of regular water waves (From Bowden, 1983)

If we want to find the wavenumber k corresponding to a certain w, we are faced with a so-called transcendental equation. It is in general impossible to turn the dispersion relation around and express k as a function w . Of course, for shallow and deep water, the approximate solutions are fully adequate. However, it is very simple to solve it as closely as we want numerically, i.e. on a computer. The FORTRAN function below solves k to a relative accuracy better than 10-6 for all w. Or you may apply: DalrymplesJavaAppletsCoastalEngineering: Linear wave kinematics

Fig. 5.3: A FORTRAN function for solving for k as a function of w and the depth h.

An approximative formula is found at:

DalrymplesJavaAppletsCoastalEngineering: Wave Calculator

....