7 PLANE WAVES
So far our waves have been waves in a channel with the spatial coordinates x and z and the time coordinate t. From now we are going to consider waves on a two dimensional ocean, waves that may travel in any direction. By a plane wave is meant a wave with infinitely long crests (maxima) and constant elevation along lines orthogonal to the travel direction (think of corrugated iron).
The general regular plane wave may be written
![]()
where x is the position vector consisting of the coordinates
(x,y) and k is called the wavenumber vector with coordinates which
we usually write ![]() . We
use kx for the scalar product of k and x.
. We
use kx for the scalar product of k and x. ![]() .
The wavenumber vector has magnitude, k, equal to the wavenumber and direction
equal to the propagation direction of the wave. Let us verify this for a wave
.
The wavenumber vector has magnitude, k, equal to the wavenumber and direction
equal to the propagation direction of the wave. Let us verify this for a wave
![]() .
.
|
|
Set k = k·a where a is a unit vector. Consider a vertical plane cut through the wave and through the origin, parallel to the unit vector a. The horizontal position vector to all points along the cut in the (x,y)-plane may be written
|
This is the familiar regular wave moving along the r-axis, that is in the direction of a.
|
|
If we now consider an arbitrary point x, we may write
|
This shows that the value of ![]() is
the same for all values of b , that is, along lines orthogonal to ,or
as stated above, along lines orthogonal to the propagation direction.
is
the same for all values of b , that is, along lines orthogonal to ,or
as stated above, along lines orthogonal to the propagation direction.
With ![]() , we may also introduce polar coordinates
, we may also introduce polar coordinates ![]() and write
and write
![]()
The propagation direction of the wave is thus given by q. In general we then have
![]()
Check what you get for q= 0°,´90°, 180°, 270°!
For a general ocean surface extending both in the x- and y-directions, our equations and boundary conditions for the surface waves must also include the y-coordinate. It is easy to see that the new linearized equations are
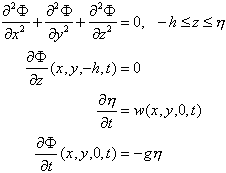
Check that the plane wave travelling along the x-axis,
![]()
and the corresponding velocity potential
![]()
still satisfy the equations! (This is easy since neither h nor F contain y!) Since there is in general nothing special with waves in the x-direction in the above equations, we therefore conclude that the general regular plane wave solution to the equations is the one above with kx replaced by k·x for an arbitrary wavenumber vector k.