In the open ocean, it is impossible to keep track on each individual wave. Actually, this does not make much sense even if we had very good instruments! What we need is a manageable way to describe essential properties of the wave conditions. Fortunately, it turns out that the linear wave theory we discussed in Part A is a good starting point. In fact, it turns out be a good model of the sea surface to consider it made up from a lot of regular plane waves. This model is called random linear wave theory. As the name suggests, the theory requires some understanding of probability theory and a very short review of the necessary concepts are introduced in Appendix A.

The first step towards the random model is to consider a surface made up by a finite sum of plane waves

where is the amplitude, and are related by the dispersion relation and is the phase. Recall that this is a solution of the linearized equations, cf. Part A, Sec. 8. Whereas the amplitudes and the wavenumbers in the sum are constant characteristics independent of where we are, the phase is more arbitrary. Actually it depends on where we choose our origin. Since it is impossible to give a unique definition of where to put an origin in the open ocean, we simply abandon to specify the phase. In random linear wave theory one thus says that the phase is arbitrary, or random. Without going into more details, one assumes that are independent stochastic variables, uniformly distributed on [0,2p]. This means that there is no relation whatsoever between the phase angles of the different waves, and that the phase angle can take any value between 0 and 2p with equal probability.

For a given x and t, set . Let us compute the expectation value and the variance of the function where is uniformly distributed on [0,2p]:

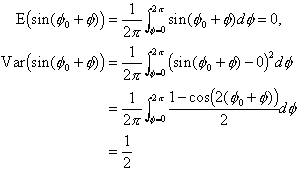
Since we have assumed that are uniformly distributed random variables, we now obtain by the rules for sums of independent stochastic variables that

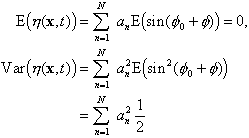
In practice, instead of a finite number of waves, one assumes that the surface is made up of infinitely many waves, all having different amplitudes and wavenumbers. It is then convenient to write replace the sumation

by an integral

.

The function signifies the "density of waves" around the wavenumber since the part of the sum to the left having wavenumbers in the area around is just . The function may also be called the variance density of the wave field for the obvious reason

(Note the shorthand notation for the integral). However, the most common name for is the wavenumber spectrum. The wavenumber spectrum and the other related spectra discussed below are the most important concepts in random linear wave theory.

Note that and that it may be considered to be a kind of "probability density" for the waves. If is concentrated around the wavenumber , this means that the wavefield is dominated by waves with wavenumber , that is, waves going in the direction with frequency . Apart from the simple case with a finite number of waves, it is not so obvious how to talk about the amplitude of individual waves in this general setting. Usually is considered to be a smooth function of . However, with a finite number of waves, will be a sum of "spikes",- socalled d-functions. In the following we shall not consider this situation but simply assume that is a well-behaved, non-negative function.

An alternative interpretation of the wave spectrum is in terms of the ocean wave surface energy pr. area unit. We recall that the sum of the kinetic and potential energy pr area unit, E, was for a regular wave with amplitude a. In the present case this generalizes to

Thus, the wave spectrum may also be seen as proportional to the wave energy distribution as a function of the wavenumber.

Since , it is possible to write the integral for the variance in (k-) polar coordinates:

Moreover, because of the dispersion relation, we may also change the variable from k to w :

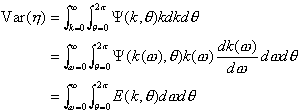
In practice, the function

is even more commonly used than and is called the directional wave spectrum. Again, it that important to note that the integral of E over w and q is equal to the variance of the surface. Note there is no extra w in the integral of E as we had for k in the integral of . This is just what has become common. The function E is often written as a product

where the angular dependent part, , is normalized such that

.

The function S is called the wave frequency spectrum or simply the spectrum. The wave frequency spectrum does not contain any information about the direction of the waves. The directional information is contained in the directional distributions, . In general, D will be dependent of w.

Practical wave analysis uses the frequency, f, instead of the angular frequency w. The definition must then be used in the dispersion relation. If we have a frequency spectrum, , then the corresponding frequency spectrum, , using f instead of w , will be

Note that

In the following we omit the ~-symbol and assume that the transformation is carried out properly.

For readers familiar with (stationary) random processes the word spectrum will be known as the Fourier transform of the correlation function. It is possible to derive the wave spectrum starting from the space-time correlation function of the ocean surface, and an assumption about linear wave theory. However, even very well known textbooks about waves confuses the wave spectrum and the spectrum of a stochastic surface. The wave spectrum as introduced above requires linear wave theory, or more precisely, that we have a well-defined dispersion relation.

We have now introduced the core of linear wave theory. In the random model we sacrifice some details of the description of the waves in that we do not specify the phase of the waves. The basic new concept we have introduced is the wavenumber spectrum Y. The spectrum is needed because we are considering a continuum of plane regular waves, but one should not forget the obvious link to the simpler case with a finite sum of regular waves. Due to the connection with the surface variance, the spectrum is in effect proportional to the distribution of wave energy as a function of wavenumber. Since we consider the wave phases as random variables, the surface becomes what is commonly denoted a random surface. The wave spectrum gives us a complete knowledge of this random surface under one additional assumption, namely when the surface is suppose to be Gaussian (There are some technicalities in the concept of a Gaussian random surface which we do not consider at the moment). Real ocean surfaces have turned out to be very closely Gaussian, but there are slight deviations, the most notable is that the wave crests are somewhat higher than the wave troughs are low. This gives the surface a certain asymmetry which is not reflected in the spectrum under normal conditions.