PART B
Random waves and wave statistics
1 INTRODUCTION
In Part A, the emphasis was on one or a few regular waves specified in terms of the wavelengths, the amplitudes and the phase factors. The angular frequency was defined by the dispersion relation. However, if we watch the sea on a windy day, the waves are far from being regular, and it is impossible to keep track of, say an individual wave crest for more than a few periods. It thus appears that the theory we have developed will be of little or no use in this situation. Whereas the theory of ocean waves as we know it from Part A was developed in the last century, a usable description of the complex sea surface at the open ocean came much later, basically after the Second World War.
The only waves in the ocean which resemble what we considered in Part A is swell generated by a distant storm. Swell can be surprisingly regular, but never pure sine waves. In order to model a sea surface consisting of a wind sea and swell, we must introduce what is commonly referred to as random waves. This is a description which, in a way, is not as detailed as the full description of the surface motion we considered in Part A. Nevertheless, linear random wave theory is basically the theory in Part A put in a random or probabilistic setting. Knowledge of elementary probability theory is therefore necessary for the understanding of the theory.
The most important concept for random waves is the wave spectrum to be defined below. Within the approximations which are built into linear wave theory itself, the spectrum basically gives us all properties we need about the waves, that is, it defines what is called the sea state.
Under normal conditions the wave spectrum and hence the sea state is likely to be constant over, say, half an hour. The properties of the sea for a constant sea state is covered by what is denoted short term wave statistics. Short term wave statistics deals with the properties of the individual waves, typically the probability distributions of wavelength, period, height and so on. All these and other concepts will be fully defined and discussed below.
For time periods longer than a few hours, the sea state is likely to vary. Variations in the sea states, are covered by a (different) random theory and described by long term wave statistics.
For coastal and ocean engineering, it is very important to know how rough conditions the structures are likely to encounter during their lifetime, and this part of the long term statistics is treated by extreme wave statistics. Extreme wave statistics provides methods to estimate how rough conditions are likely to happen at a given location over a time span of, say 100 years.
In Part B we shall introduce some of the central topics of random waves starting with the wave spectrum and the main wave parameters. Short and long term statistics are treated briefly, and finally some points of extreme wave statistics are introduced.
2 RANDOM WAVES AND WAVE SPECTRA
In the open ocean, it is impossible to keep track on each individual wave. Actually, this does not make much sense even if we had very good instruments! What we need is a manageable way to describe essential properties of the wave conditions. Fortunately, it turns out that the linear wave theory we discussed in Part A is a good starting point. In fact, it turns out be a good model of the sea surface to consider it made up from a lot of regular plane waves. This model is called random linear wave theory. As the name suggests, the theory requires some understanding of probability theory and a very short review of the necessary concepts are introduced in Appendix A.
The first step towards the random model is to consider a surface made up by a finite sum of plane waves
![]()
where ![]() is the amplitude,
is the amplitude, ![]() and
and ![]() are related by the dispersion relation and
are related by the dispersion relation and ![]() is the phase. Recall that this is a solution of the linearized equations, cf. Part A, Sec. 8. Whereas the amplitudes and the wavenumbers in the sum are constant characteristics independent of where we are, the phase is more arbitrary. Actually it depends on where we choose our origin. Since it is impossible to give a unique definition of where to put an origin in the open ocean, we simply abandon to specify the phase. In random linear wave theory one thus says that the phase is arbitrary, or random. Without going into more details, one assumes that
is the phase. Recall that this is a solution of the linearized equations, cf. Part A, Sec. 8. Whereas the amplitudes and the wavenumbers in the sum are constant characteristics independent of where we are, the phase is more arbitrary. Actually it depends on where we choose our origin. Since it is impossible to give a unique definition of where to put an origin in the open ocean, we simply abandon to specify the phase. In random linear wave theory one thus says that the phase is arbitrary, or random. Without going into more details, one assumes that ![]() are independent stochastic variables, uniformly distributed on [0,2
are independent stochastic variables, uniformly distributed on [0,2
For a given x and t, set ![]() . Let us compute the expectation value and the variance of the function
. Let us compute the expectation value and the variance of the function ![]() where
where ![]() is uniformly distributed on [0,2
is uniformly distributed on [0,2
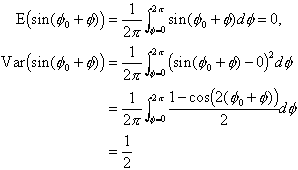
Since we have assumed that ![]() are uniformly distributed random variables, we now obtain by the rules for sums of independent stochastic variables that
are uniformly distributed random variables, we now obtain by the rules for sums of independent stochastic variables that
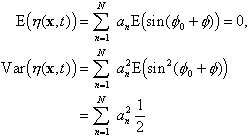
In practice, instead of a finite number of waves, one assumes that the surface is made up of infinitely many waves, all having different amplitudes and wavenumbers. It is then convenient to write ![]() replace the sumation
replace the sumation
![]()
by an integral
![]() .
.
The function ![]() signifies the "density of waves" around the wavenumber
signifies the "density of waves" around the wavenumber ![]() since the part of the sum to the left having wavenumbers in the area
since the part of the sum to the left having wavenumbers in the area ![]() around
around ![]() is just
is just ![]() . The function may also be called the variance density of the wave field for the obvious reason
. The function may also be called the variance density of the wave field for the obvious reason
![]()
(Note the shorthand notation for the integral). However, the most common name for ![]() is the wavenumber spectrum. The wavenumber spectrum and the other related spectra discussed below are the most important concepts in random linear wave theory.
is the wavenumber spectrum. The wavenumber spectrum and the other related spectra discussed below are the most important concepts in random linear wave theory.
Note that ![]() and that it may be considered to be a kind of "probability density" for the waves. If
and that it may be considered to be a kind of "probability density" for the waves. If ![]() is concentrated around the wavenumber
is concentrated around the wavenumber ![]() , this means that the wavefield is dominated by waves with wavenumber
, this means that the wavefield is dominated by waves with wavenumber ![]() , that is, waves going in the direction
, that is, waves going in the direction ![]() with frequency
with frequency ![]() . Apart from the simple case with a finite number of waves, it is not so obvious how to talk about the amplitude of individual waves in this general setting. Usually
. Apart from the simple case with a finite number of waves, it is not so obvious how to talk about the amplitude of individual waves in this general setting. Usually ![]() is considered to be a smooth function of
is considered to be a smooth function of ![]() . However, with a finite number of waves,
. However, with a finite number of waves, ![]() will be a sum of "spikes",- socalled
will be a sum of "spikes",- socalled
An alternative interpretation of the wave spectrum is in terms of the ocean wave surface energy pr. area unit. We recall that the sum of the kinetic and potential energy pr area unit, E, was ![]() for a regular wave with amplitude a. In the present case this generalizes to
for a regular wave with amplitude a. In the present case this generalizes to
![]()
Thus, the wave spectrum may also be seen as proportional to the wave energy distribution as a function of the wavenumber.
Since ![]() , it is possible to write the integral for the variance in (k-) polar coordinates:
, it is possible to write the integral for the variance in (k-) polar coordinates:
![]()
Moreover, because of the dispersion relation, we may also change the variable from k to
w :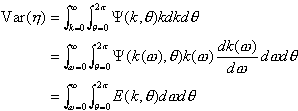
In practice, the function
![]()
is even more commonly used than ![]() and is called the directional wave spectrum. Again, it that important to note that the integral of E over
and is called the directional wave spectrum. Again, it that important to note that the integral of E over
![]()
where the angular dependent part, ![]() , is normalized such that
, is normalized such that
![]() .
.
The function S is called the wave frequency spectrum or simply the spectrum. The wave frequency spectrum does not contain any information about the direction of the waves. The directional information is contained in the directional distributions, ![]() . In general, D will be dependent of
. In general, D will be dependent of
Practical wave analysis uses the frequency, f, instead of the angular frequency w. The definition ![]() must then be used in the dispersion relation. If we have a frequency spectrum,
must then be used in the dispersion relation. If we have a frequency spectrum, ![]() , then the corresponding frequency spectrum,
, then the corresponding frequency spectrum, ![]() , using f instead of w , will be
, using f instead of w , will be
![]()
Note that
![]()
In the following we omit the ~-symbol and assume that the transformation is carried out properly.
For readers familiar with (stationary) random processes the word spectrum will be known as the Fourier transform of the correlation function. It is possible to derive the wave spectrum starting from the space-time correlation function of the ocean surface, and an assumption about linear wave theory. However, even very well known textbooks about waves confuses the wave spectrum and the spectrum of a stochastic surface. The wave spectrum as introduced above requires linear wave theory, or more precisely, that we have a well-defined dispersion relation.
We have now introduced the core of linear wave theory. In the random model we sacrifice some details of the description of the waves in that we do not specify the phase of the waves. The basic new concept we have introduced is the wavenumber spectrum Y. The spectrum is needed because we are considering a continuum of plane regular waves, but one should not forget the obvious link to the simpler case with a finite sum of regular waves. Due to the connection with the surface variance, the spectrum is in effect proportional to the distribution of wave energy as a function of wavenumber. Since we consider the wave phases as random variables, the surface becomes what is commonly denoted a random surface. The wave spectrum gives us a complete knowledge of this random surface under one additional assumption, namely when the surface is suppose to be Gaussian (There are some technicalities in the concept of a Gaussian random surface which we do not consider at the moment). Real ocean surfaces have turned out to be very closely Gaussian, but there are slight deviations, the most notable is that the wave crests are somewhat higher than the wave troughs are low. This gives the surface a certain asymmetry which is not reflected in the spectrum under normal conditions.
Exercise 2.1: Find the surface variance ( Var(h) ) if
![]()
and ![]() .
.
Exercise 2.2: A very simple form of the wavenumber spectrum for wind generated waves is
![]()
where q is the direction of k, i.e. ![]() . Determine the corresponding directional spectra as functions of w and q in deep and very shallow water.
. Determine the corresponding directional spectra as functions of w and q in deep and very shallow water.
Review questions:
1. What is the wavenumber spectrum and how do we obtain the variance of the sea surface
from the spectrum?
2. What is the sea state?
3. How can we consider the surface as an infinite sum of plane waves?
4. How do we move from the wavenumber spectrum to the directional spectrum?
5. The directional spectrum is often written as a product of two functions, how?
3 SEA STATE PARAMETERS AND ENGINEERING WAVE SPECTRA
We recall that the sea state is the condition of the ocean surface considered as a stochastic field and characterized by the wave spectrum. This is the modern use of the word. Traditionally sea state is a scale for the average wave height somewhat similar to the Baufourt scale for wind.
The most complete wave spectra we are considering are the wavenumber spectrum ![]() , and the directional spectrum
, and the directional spectrum ![]() . As discussed in the previous section, practical wave analysis uses the frequency f instead of
. As discussed in the previous section, practical wave analysis uses the frequency f instead of ![]() . Moreover, engineers tend to use the directional spectrum instead of the wavenumber spectrum. Below we shall follow this convention and write the directional spectrum as
. Moreover, engineers tend to use the directional spectrum instead of the wavenumber spectrum. Below we shall follow this convention and write the directional spectrum as ![]() .
.
The square root of the variance of the surface, is the standard deviation of the surface. The standard deviation is a common measure for the variations about the mean and is thus a reasonable scale for the surface height variations. For historical reasons it has become a standard to denote four times the standard deviation the significant wave height. Significant wave height is written Hs, SWH, Hm0 or a number of other possibilities. We shall write Hm0 for a special reason. Related to the spectrum is a series of characteristic numbers called the spectral moments. These numbers, denoted ![]() are defined as
are defined as
![]()
The spectral moment ![]() is just the variance of the surface and hence
is just the variance of the surface and hence
![]()
which is the reason for the notation. The "old" definition of the significant wave height was the mean of the one third largest waves in the sea, - a definition which is not very easy to apply! The significant wave height is without doubt the most important sea state parameter. Note that when computed from actual wave measurements, the new definition is about 5% higher than the old definition.
The frequency for which ![]() attains its maximum is called the peak wave frequency.
attains its maximum is called the peak wave frequency.
![]() .
.
The inverse of ![]() is also used, and is called the peak period,
is also used, and is called the peak period,
![]() .
.
An equally common period parameter is the mean wave period, ![]() , also denoted
, also denoted ![]() :
:
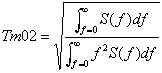
We shall return to the most important directional wave parameters after we have discussed some engineering forms for the wave spectra. The wave spectrum for a given sea state may be measured by various wave recording devices and the functions we are going to present below have been found to fit the measurements.
The most well known functional form of S is the so-called Pierson-Moskowitz spectrum
![]() .
.
In the original work by Pierson and Moskowitz both Aand B were related to the wind speed 19.5 m (!) above the mean sea surface, but today Aand B are in some way related to the main sea state parameters. One possibility is to set
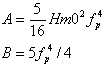
Exercise 3.1: Check that for the Pierson-Moskowitz spectrum with A and B defined as above
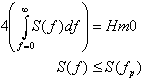
Another popular form has been the JONSWAP spectrum which is defined by the somewhat curious expression
![]()
The JONSWAP spectrum is thus a Pierson-Moskowitz like spectrum multiplied by an extra "peak enhancement factor"
![]()
Verify that this factor is equal to
g when
Fig. ????: The Pierson-Moskowitz spectrum and the standard JONSWAP spectrum. Dimensionless functions with ![]() and
and ![]() .
.
Fig. ???: Example of a measured frequency spectrum for a heavy sea state. Note the use of a logarithmic vertical axis
Fig. ???: Non-dimensional measured spectrum compared to the JONSWAP spectrum.
In many practical situations, the directions of the waves are also of great interest and the directional part of the spectrum is now just at the point of being included in engineering analyses. We recall the directonal spectrum as
![]() .
.
The directional distribution, ![]() , may be understood as the distribution of wave energy for a given frequency
, may be understood as the distribution of wave energy for a given frequency ![]() over the directions
over the directions ![]() . Note that D is generally also a function of
. Note that D is generally also a function of ![]() . This reflects the fact that there most of the time exists several systems of waves simultaneously. High frequency wind sea and low frequency swell from different direction is a common case.
. This reflects the fact that there most of the time exists several systems of waves simultaneously. High frequency wind sea and low frequency swell from different direction is a common case.
Since ![]() is a periodic function of
is a periodic function of ![]() it is convenient to introduce the Fourier series
it is convenient to introduce the Fourier series
![]() .
.
Note that this expression already fulfils already
![]()
It turns out that many of the common instruments that measure directional wave spectra actually measure Fourier coefficients (as a function of the frquency) rather than the directional distribution itself.
The facts that ![]() and has integral equal to 1 suggests that we may think of D as a kind of probability distribution over direction. We recall that the most important parameters for a probability distribution are the mean and the standard deviation. Usually, the stochastic variables we meet are taking integer or real numbers as values, but in the present case, where
and has integral equal to 1 suggests that we may think of D as a kind of probability distribution over direction. We recall that the most important parameters for a probability distribution are the mean and the standard deviation. Usually, the stochastic variables we meet are taking integer or real numbers as values, but in the present case, where ![]() the definitions of the mean and the standard deviations have to be modified. It turns out that the most common definitions, which in the present case are denoted the mean direction and the directional spread for D are defined directly in terms of the Forier coefficients. The mean direction is defined as
the definitions of the mean and the standard deviations have to be modified. It turns out that the most common definitions, which in the present case are denoted the mean direction and the directional spread for D are defined directly in terms of the Forier coefficients. The mean direction is defined as
![]() ,
,
that is, the direction of the vector with components ![]() , or the direction (argument) of the complex number
, or the direction (argument) of the complex number
![]() .
.
Note that this also implies that ![]() and
and ![]() .
.
For the directional spread (or rather the directional variance) we would like to have an expression
![]()
which, however, is not periodic. One possible choice is instead to use ![]() which is approximately equal to
which is approximately equal to ![]() when
when ![]() small. This gives us
small. This gives us
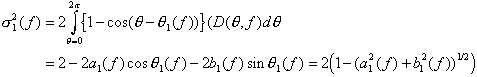
which is ususally written as ![]() (suppressing the dependence of frequency). In summary, both the mean directiona and the directional spread may thus be derived from the first pair of Fourier coefficients.
(suppressing the dependence of frequency). In summary, both the mean directiona and the directional spread may thus be derived from the first pair of Fourier coefficients.
When it comes to actually describing the directional distributions, seveal functional forms are in use. An often used form is the cos-2s-distribution
![]()
where ![]() and
and ![]() is a normalization factor such that the integral becomes equal to 1. By means of the integration formula
is a normalization factor such that the integral becomes equal to 1. By means of the integration formula
*********
it is possible to show
N(S)=---..,,
s = ..
Fig. ***: The cos-2s-distribution for several values of s.
Exercise 3.2: Show that the JONSWAP spectrum reduces to the Pierson-Moskowitz spectral form when
g = 1. Also show that the Pierson-Moskowitz spectrum is approximately proportional toExercise 3.3: Consider the directional spectrum
![]()
Find expressions for Hm0, Tm02, ![]() and
and ![]() (Hint: Determine
(Hint: Determine ![]() and
and ![]() ).
).
Exercise 3.3: Consider the following simple directional distribution
![]()
Determine ![]() and
and ![]() .
.
Exercise 3.4: Consider the directional spectrum
![]()
Find expressions for Hm0, Tm02, ![]() and
and ![]() (Hint: Determine
(Hint: Determine ![]() and
and ![]() ).
).
Review questions:
1. How do we pass from
w to2. How is significant wave height, peak period, mean period, mean direction and
directional spread defined?
3. What is the Pierson-Moskowitz spectrum?
Warning: This very short introduction is just for refreshing the concepts. Consult a textbook for a much more complete introduction.
The most sentral concept in probability theory is that of a random (or stochastic) variable. A random variable is actually a function, but contrary to an ordinary function where we put in an argument and compute an output value, we have no knowledge about the input (Some like to think of a god putting in the value). All we can see is the output and we have to deduce all properties of the function by observing the output. It turns out that what we have to determnine is the distribution of the outcomes. For a real number valued random function the distribution function is defined
![]()
where X symbolizes both the function and the values, and "Prob" means the probability (or the fraction of times) that the outcome is less or equal to x. If the outcome is an angle between 0 and 2
p the definition is similar. The derivative of distribution function is called the probability density,![]() . Note that
. Note that ![]() and
and ![]() . For a real number valued random function X the expectation is by
. For a real number valued random function X the expectation is by
![]()
and the variance of X,
![]() .
.
If ![]() is a function of X then
is a function of X then ![]() . The squareroot of the variance is called the standard deviation.
. The squareroot of the variance is called the standard deviation.
Two stochastic variables have a joint distribution function ![]() and a joint probability density
and a joint probability density ![]() . The covariance between two stochastic variables X and Y is defined as
. The covariance between two stochastic variables X and Y is defined as
![]() .
.
X and Y are independent if ![]() . Then
. Then ![]() and we say that X and Y are uncorrelated. Note also that
and we say that X and Y are uncorrelated. Note also that ![]() .
.
The most important rules concerning the sums of stochastic variables are
![]()
and, if the variables are uncorrelated,
![]()
Below we shall consider a stochastic phase angle ![]() uniformly distributed on [0,2π]. This means that its probability density is
uniformly distributed on [0,2π]. This means that its probability density is ![]() . Consider now the random function
. Consider now the random function ![]() , By the rules we just have introduced we have
, By the rules we just have introduced we have

These expressions were used in Section. 1