| Øving 4 |
Naturlaster/miljø |
Utlevert 12/2-99 |
Innleveres 1/3-99 |
| Spektral-estimering |
Disk.: 23/2 & 26/2 |
||
|
Gj.g.: 6/3- 99 |
|||
Øvingen er en diskusjon av tidevannsdata og eksempel på hvordan vi kan bruke FFT til å bestemme hvilke frekvenser som er til stede i et signal. Bruk EXCEL eller et annet IT-verktøy. Beskrivelsen nedenfor forutsetter bruk av EXCEL.
Start EXCEL
1) I kolonne A (Ark 1), legg inn tid fra t=0 til 4 uker i steg på 30 minutter . Bruk time som enhet dvs 0.0, , 0.5, 1.0,....672 timer.
2)Kopier navn og frekvenser for de harmoniske komponentene fra tabell 2.5 i kompendiet inn i Ark 2 og beregn perioden for komponentene. Legg disse verdiene i kolonne C i Ark 2.
3) Hvilke frekvenser kan en ta med i en harmonisk analyse når måleperioden er 4 uker? Begrunn svaret! Svaret: Komponentene som kan tas med er merket med x i tabellen nedenfor:
|
j |
Symb |
o/h |
Hj cm |
gj o |
|
|
1 |
M2 |
28.9841 |
x |
91.4 |
328 |
|
2 |
S2 |
30 |
x |
32.1 |
5 |
|
3 |
N2 |
28.4397 |
x |
18.2 |
307 |
| K2 |
30.0821 |
- |
|||
|
4 |
K1 |
15.041 |
x |
6.8 |
179 |
|
5 |
O1 |
13.943 |
x |
5.4 |
51 |
| P1 |
14.9589 |
- |
|||
|
6 |
Mf |
1.098 |
x |
2.7 |
187 |
| Mm |
0.0909 |
- |
|||
| Ssa |
0.0802 |
- |
4) Bruk de utplukkede frekvensene j=1-6 til å simulere en tidevann data serie for de 4 ukene.
For hver av komponentene beregn
![]()
for de diskrete tidspunktene og legg resultatet i kolonne (1+j) i Ark 1. (dvs kolonne B for j=1, C for kolonne j=2 osv) . Til slutt i kolonne 8 (H) summer bidragene. Altså
![]()
med konstanter som vist i tabellen over.
5) Plott alle tidsseriene 1-6 (B-G) som funskjoner av tiden for t=0 til t=72 timer dvs (3 døgn) i samme diagram.
6) Plott ![]() for hele perioden.
Svevningen i signalet kan forklares ut fra to nabofrekvenser. Hva er perioden i
svevningen. Hvilke nabofrekvenser tror du gir opphavet til denne svevningen?
for hele perioden.
Svevningen i signalet kan forklares ut fra to nabofrekvenser. Hva er perioden i
svevningen. Hvilke nabofrekvenser tror du gir opphavet til denne svevningen?
7) Dersom du ikke hadde kjent til hvordan tidsserien hadde blitt laget, hvilke frekvenser ville du ha gjettet på var i signalet?
8) Vi skal nå gå over på en DFT analyse av signalet
![]() . EXCEL har en FFT rutine. Du
finner den under tools (verktøy) data analysis . Start FFT og
følg anvisningene og bruk 1024 datapunkter dvs 512 timer. Rutinen i
EXCEL definerer Fouriertransformen motsatt av det Newland gjør. Dvs
når vi ønsker en FFT i EXCEL må det krysses av i feltet for
invers. Resultatet blir en serie med komplekse tall som er DFT-verdiene for
. EXCEL har en FFT rutine. Du
finner den under tools (verktøy) data analysis . Start FFT og
følg anvisningene og bruk 1024 datapunkter dvs 512 timer. Rutinen i
EXCEL definerer Fouriertransformen motsatt av det Newland gjør. Dvs
når vi ønsker en FFT i EXCEL må det krysses av i feltet for
invers. Resultatet blir en serie med komplekse tall som er DFT-verdiene for
![]() som vi betegner Xk.
1. tall er for frekvens k=0 dvs
som vi betegner Xk.
1. tall er for frekvens k=0 dvs ![]() som representerer middelverdien i signalet. Den neste verdien er for frekvens
som representerer middelverdien i signalet. Den neste verdien er for frekvens
![]() 1/512 pr time, neste igjen er
1/512 pr time, neste igjen er
![]() 2/512 pr time osv som
2/512 pr time osv som
![]() k/512. Omregnet i grader pr time
blir det hhv 0,
k/512. Omregnet i grader pr time
blir det hhv 0, ![]() 360/512,
360/512,
![]() 720/512 osv. som
720/512 osv. som
![]() 360k/512, slik at f eks den 41.
frekvensen gir
360k/512, slik at f eks den 41.
frekvensen gir ![]() 360*40/512=
360*40/512=![]() 28.1o/time.
28.1o/time.
9) Beregn ![]() ved
å bruke funksjonen IMABS Xk . Legg verdiene
i en egen kolonne. Fra DFT-analysen i Newland (1993) vet vi at
|Xj| , med j slik at DFT-frekvensen er i
nærheten av frekvensen til tidevannskomponenten, er sammenlignbar med
Hj/2 (jfr oppgave 10.1(iii)) hos Newland og
altså Sj sammenlignbar med
Hj2/4. Sjekk dette!
Ak er amplituden til spektralkomponent k og
Hj amplituden til tidevannskomponent j.
ved
å bruke funksjonen IMABS Xk . Legg verdiene
i en egen kolonne. Fra DFT-analysen i Newland (1993) vet vi at
|Xj| , med j slik at DFT-frekvensen er i
nærheten av frekvensen til tidevannskomponenten, er sammenlignbar med
Hj/2 (jfr oppgave 10.1(iii)) hos Newland og
altså Sj sammenlignbar med
Hj2/4. Sjekk dette!
Ak er amplituden til spektralkomponent k og
Hj amplituden til tidevannskomponent j.
10) Lag så en kolonne med frekvenser for k=0,..... Plott Ak mot frekvens for frekvenser opp til 40 grader/time . Får du noe tilsvarende dette?
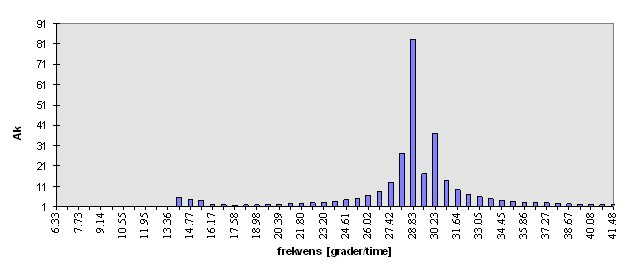
11) Finner du igjen frekvensene gitt i tabellen over? Nei! Pga det valgte analyseintervallet 512 timer har ikke FFT truffet eksakt på de gitte frekvenser. "Energien" blir derfor smurt litt utover på frekvensene i nærheten. Dette kalles lekkasje.
12) Vi skal nå lavpass filtrere signalet. Se appendix D. Dette kan vi
gjennomføre ved Invers FFT (IFFT). Vi fjerner spektralbidrag
høyere enn cut-off frekvensen ved å sette fourierkopmponentene lik
null og så utføres IFFT. Start Fourier-analysen i EXEL og la
vær og kryss ut feltet invers. Velg cut-off-frekvensen lik
20o/time.
Lavpassfiltrering kan også utføres ved bruk av glidende
middelverdi over 2n+1 registreringer (Jfr Appendix D). Bestem den
n som gir oss en cut-off frekvens tilnærmet lik
20o/time og beregn glidende middel tidsserien. Ta DFT av denne og
sammenlign Fourierkomponentene med de fra den opprinnelige serien med de
høyeste frekvensene satt lik null. Kommenter.
13) Beregn differansetidsserien mellom opprinnelig og lavpassfiltrert. Dette blir nå en høypassfiltrert tidsserie. Beregn DFT til denne. Nå skal energien på de laveste frekvensene være borte, stemmer det?
14) Bruk Ak-ene fra punkt 10) og plott
estimatet for spektraltettheten ![]() (ensidig spektyer) til tidserien. Dvs verdiene må skaleres
slik at integralet over spektret blir lik totalvarieansen. Skriv ned
sammenhengen mellom Ak og
(ensidig spektyer) til tidserien. Dvs verdiene må skaleres
slik at integralet over spektret blir lik totalvarieansen. Skriv ned
sammenhengen mellom Ak og
![]() . Enheten til
spektraltetthetsfunskjonen skal være m2s/rad.
. Enheten til
spektraltetthetsfunskjonen skal være m2s/rad.